Reading Light Bands

What Are Light bands?

Light bands formed by using an optical flat and a monochromatic light source represent an inexpensive yet accurate method of checking surface flatness. The monochromatic light on which the following diagrammatic interpretations are based comes from a Sodium filled tube source which eliminates all colours except a “yellowish” orange.

One wave length of light from this source measures 23.2 millionths of an inch. However, since only one half of the wave is used in the measurement procedure the unit of measure is one half of 23.2 or 11.6 millionths of an inch (.0000116”). The dark bands seen beneath the optical flat are not light waves, but interference lines caused by the reflection from the two surfaces. It is these dark bands that are used in measuring the flatness of the surface.

The band unit of measure is .0000116”: that is between the centre of one dark band and the centre of the next dark band, the surface of the workpiece has risen or fallen 11.6 millionths of an inch (.0000116”) in relation to the optical flat.

(note: the optical flat must always be more accurate than the surface being inspected).

How to read light bands

Interpretation of interference band patterns is fairly simple. The illustrations show basic variations from an absolute flat surface and how these variations indicate a specific flatness of the measured surface.

The workpiece must be clean, dry and have a reflective surface if light bands are to be visible. The closer the flat to the work the wider the bands will be. Many fine bands indicate that dust or dirt is between the flat and the work making correct interpretation difficult. The line, or point, of contact referred to in the illustrations is the line, or point, at which the air wedge between the optical flat and the work is thinnest. To determine the line, or point, of contact, the flat should be pressed down at various spots above the edges of the work. If the bands remain the same along one particular edge, that edge forms the line, or point, of contact. If the bands tend to broaden and become fewer in number – the opposite edge forms the line, or point, of contact.

The bands shown under the monochromatic light and optical flat form a topographical map of the surface. Bands which curve toward the line, or point, of contact indicate a concave surface and bands that curve away indicate a convex condition.

We do not attempt to explain why interference bands are formed only how to correctly interpret them.

Sample Flatness Interpretations

Drawings no. 1 – 6 show sample light band readings on a rectangular workpiece. Straight, parallel, equally spaced light bands indicate true flatness. As the workpiece becomes less flat (concave or convex) the bands will show more curvature.

In all cases the basis of comparisons is an imaginary line tangent to the band and parallel to the line of contact between the workpiece and the optical flat. The number of bands intersected by the tangent line indicates the variation from true flatness over the area of the workpiece.

Rectangular pieces

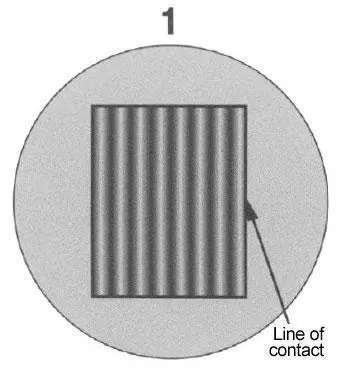
Straight, parallel and equally spaced bands show that the surface is perfectly flat within one millionth of an inch.

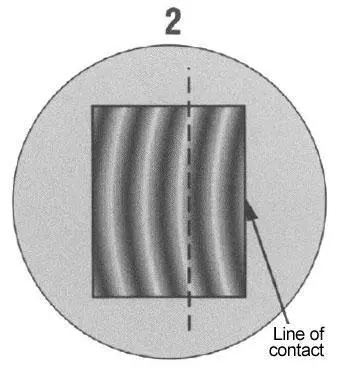
Bands do not curve enough for tangent lines to intersect one full band. Curvature of bands is equal to one half the distance from one band to the next or .0000058” (5.8 millionths of an inch) out of flat. Curvature away from line of contact indicates part is convex.

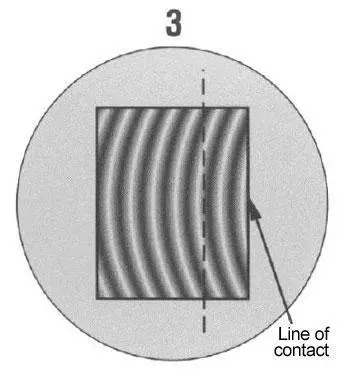
Tangent line intersects one full band showing part one full band, or .00001162 (11.6 millionths of an inch) out of flat. Again curvature away from line of contact indicates part is convex.

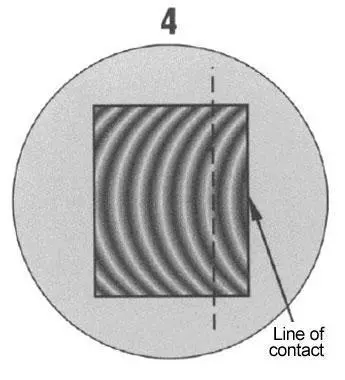
Tangent line intersects two bands showing part to be two bands or .0000232” (23.2 millionths of an inch) out of flat.

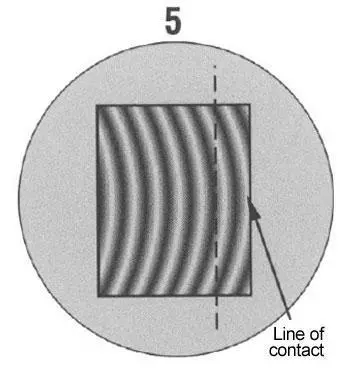
Curvature of lines toward point of contact indicates part is concave. Tangent line intersecting one full band indicates part is one band or .0000116” (11.6 millionths of an inch) out of flat.

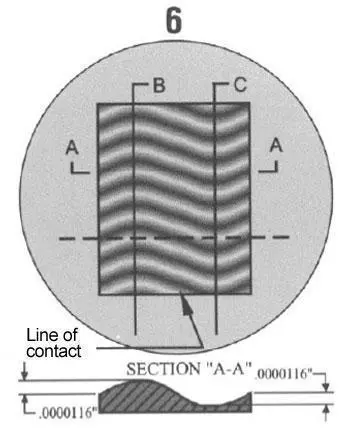
Two way curve shows part to have a ridge along line “B-B” and valley along line “C-C” of .0000116” in each case as shown on section “A-A”. This is a simple example of topographical map effect of monochromatic light and optical flat. Shown in this position to illustrate relationship to section “A-A”.

Circular pieces

Straight parallel bands show that surface is perfectly flat within one millionth of an inch.

Imaginary tangent line intersects the interference band immediately above it. This shows the sides to be low one band or .0000116” (11.6 millionths of an inch convex).

Improper Lapping

Light band readings are a very valuable way to check for improper lapping techniques, incorrect vehicle and abrasive ratios, or faulty equipment.

Looking at the two examples above. (Nº 7) Straight, parallel, equally spaced bands indicate a surface that is flat within .000001”. Bands that fall off at the outside edge of the work indicate rounded edges. This may be caused by improper polishing, incorrect vehicle abrasive ratios or excessive down pressure. (Nº 8) A falling off and break in the light band pattern indicate a low spot on the lapped surface. A longer lapping cycle may be necessary even though the major portion of the surface shows straight, parallel bands.

Convex and Concave Surfaces

The shown examples indicate exaggerated convex and concave conditions. If the work is convex, pressure near the edge will cause the flat to roll on the work and the bull’s-eye centre of the pattern will tend to move toward the point of pressure. If the work is concave, pressure at the centre will bend the flat to more closer assume the shape of the work and the circles will broaden and decrease in number.

A bulls-eye light band pattern indicates a spherical surface which may be either concave or convex. The high or low points are under the circular point of contact.